12va Clase Métodos Numéricos

Ejercicio:

Dados los datos,

1. Graficar

>> X=(-2:0.5:7)';

>> Y=[86.6;80.9;78;75.9;76.3;77.1;78.2;78.1;78.3;76.8;73.1;68.2;62;52.9;43;32.1;21;11.4;4.8];

>> plot(X,Y,'*');

>>

2. Decidir si vale la pena intentar un ajuste linear, cuadrático o cúbico y ajustar los parámetros, graficar la fucnión hallada junto con los datos, hallar el error relativo

>> A=[X X.^0];

>> B=[X.^2 X X.^0];

>> C=[X.^3 X.^2 X X.^0];

>> a=pinv(A)*Y;

>> b=pinv(B)*Y;

>> c=pinv(C)*Y;

>> Fa=@(x) a(1)*X+a(2);

>> Fa=@(X) a(1)*X+a(2);

>> Fb=@(X) b(1)*X.^2+b(2)*X +b(3);

>> Fc=@(X) c(1)*X.^3+c(2)*X.^2+c(3)*X+c(4);

>> norm(Y-Fa(X))/norm(Y)

ans =

    0.1790

>> norm(Y-Fb(X))/norm(Y)

ans =

    0.0674

>> norm(Y-Fc(X))/norm(Y)

ans =

    0.0498

>>plot(X,Y,'*',X,Fa(X),X,Fb(X),X,Fc(X))

3. En caso de que parezca necesario probar con un polinomio de grado mayor.

>> D=[X.^4 X.^3 X.^2 X X.^0];

>> d=pinv(D)*Y;

>> Fd=@(X) d(1)*X.^4 + d(2)*X.^3+d(3)*X.^2 +d(4)*X + d(5);

>> norm(Y-Fd(X))/norm(Y)

ans =

    0.0107

>> plot(X,Y,'*',X,Fd(X))

>>
 

Funciones especiales de Matlab para ajustes polinómicos (solamente)

En vez de:

>> D=[X.^4 X.^3 X.^2 X X.^0];

>> d=pinv(D)*Y;

Puedo escribir:

>> d=polyfit(X,Y,4);

En vez de:

>> Fd=@(X) d(1)*X.^4 + d(2)*X.^3+d(3)*X.^2 +d(4)*X + d(5);

Puedo escribir:

>> Fd=@(X) polyval(d, X);

Ejercicio:

1. Graficar

>> X=(0:0.01:8.99)';

>> Y=dato';

>> plot(X,Y,'*')

b) Con el basic fitting probar polinomios y comparar.

Prueba con grado 10.

c) Con polyfit y polyval hallar el ajuste polinomico de grado 10 y el error relativo.

>> e=polyfit(X,Y,10);

Warning: Polynomial is badly conditioned. Add points with distinct X

        values, reduce the degree of the polynomial, or try centering

        and scaling as described in HELP POLYFIT.

> In polyfit at 80

>> Fe=@(X)polyval(e,X);

>> plot(X,Y,'*',X,Fe(X))

>> norm(Y-Fe(X))/norm(Y)

ans =

    0.1695

>>

d) Probar ajuste con:
F1(X)= sin(X*pi)

F2(X)=cos(X*pi)

F3(X)=X^2

F4(X)=X

F5(X)=1

>> F=[sin(X.*pi) cos(X.*pi) X.^2 X X.^0];

>> f=pinv(F)*Y;

>> Ff=@(X) f(1)*sin(X.*pi)+f(2)*cos(X.*pi)+f(3)*X.^2+f(4)*X+f(5);

>> norm(Y-Ff(X))/norm(Y)

ans =

    0.0915

>> plot(X,Y,'*',X,Ff(X))

EXPONENCIAL:

Si los puntos sugieren por ejemplo un comportamiento exponencial, debería aproximar con una ecuacion del tipo

Y=ka^X= e^pX+q

Donde p=lna y q=lnk

Puedo aplicar logaritmo a ambos lados:

ln(Y)=ln(ka^X)

ln(k)+ln(a^X)=ln(Y)

ln(a)*x + ln(k)*1=ln(Y)

Digamos b(1)=ln(a) b(2)=ln(k)

Hagamos un ejemplo:

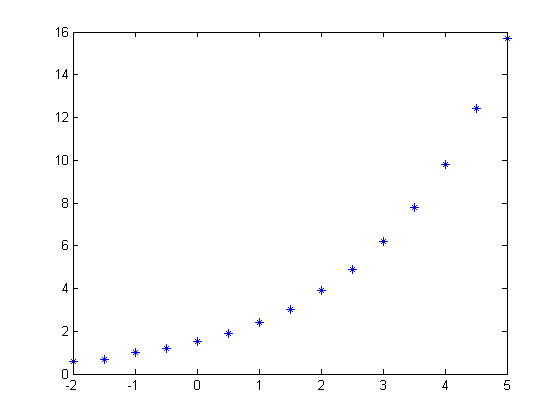
1. Graficar y observar que un ajuste exponencial parece adecuado (y=ka^x)
2. Hallar k y a declarar F=@(X)k*a.^X;
3. Graficar plot(X,Y,’*’,X,F(X)) hallar error relativo de ajuste.

>> X=(-2:0.5:5)’;

>> Y=[0.6;0.7;1;1.2;1.5;1.9;2.4;3;3.9;4.9;6.2;7.8;9.8;12.4;15.7];

>> plot(X,Y,'*')

>> b=polyfit(X,log(Y),1)

b =

    0.4688    0.4114

>> k=exp(b(2));

>> a=exp(b(1));

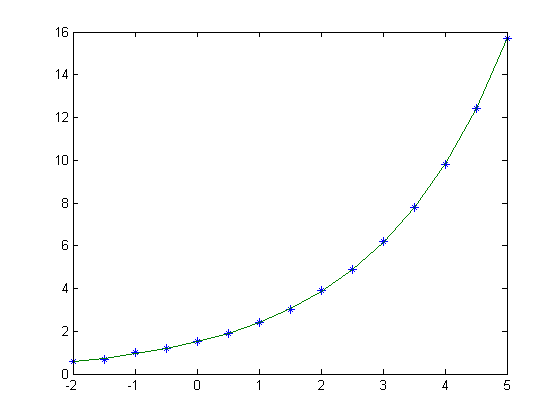
>> F=@(X) k*a.^X;

>> plot(X,Y,'*',X,F(X))

>> norm(Y-F(X))/norm(Y)

ans =

    0.0051

>>

11va Clase Métodos numéricos

Métodos numéricos 25/9/17

Repaso:

Sistemas lineales con más ecuaciones que incognitas, AKA “Sobredeterminados”

M ecuaciones

N incognitas

M>N

A*X=b

MxN

“De rango completo” es decir que el rango es N.

Estos sistemas suelen no tener solución. Habíamos visto que si lo pensamos en 3D, las soluciones posibles se nos presentan en un plano, que puede o no tener el punto solución deseado.

Lo mas probable es que un punto dado no esté en el plano de la imagen.

Como alternativa frente a este problema de inexistencia de una solución exacta de X que cumpla AX=b, se busca acercarse al punto de la imagen que menos difiera del plano de imagen.

Esto se logra con la técnica de cuadrados mínimos.

Se busca un Xcm tal que ||AXcm-b|| sea mínimo ->0.

Prop: La solución de cuadrados mínimos de AX=b coincide con la solución exacta de (A’A)X=A’b

Por lo tanto usamos esta proposición para encontrar la mejor solución Xcm al problema.

(A’A)X=A’b

Xcm=(A’A)^(-1)*A’*b

>>Xcm=resolver_chol(A’A,A’b);

(A’A) es simétrica y definida positiva. Podemos y deberíamos usar cholesky para resolver este tipo de sistemas.

Resulta que sistemas sobredeterminados, no se puede usar la propiedad

A^(-1) *A = I

A*A^(-1) = I

Defino Pseudo Inversa Izquierda::

A^(-1) izq = (A’A)^(-1)*A’

A^(-1) izq*A=I

PERO

A* A^(-1) izq no es igual a I, por mas que su dimencion es mxm.

[2 -1 3;3 1 5; 6 1 2;-1 0 8]

A_1_izq=((A'*A)^(-1))*A'

Ejemplos:

>> A=[2 -1 3;3 1 5; 6 1 2;-1 0 8];

>> A_1_izq=((A'*A)^(-1))*A'

A_1_izq =

    0.1167    0.0023    0.1143   -0.0738

   -0.6401    0.2778    0.0821    0.0459

    0.0259    0.0376   -0.0116    0.0947

>> A_1_izq*A

ans =

    1.0000    0.0000   -0.0000

   -0.0000    1.0000    0.0000

   -0.0000    0.0000    1.0000

>> pinv(A)

ans =

    0.1167    0.0023    0.1143   -0.0738

   -0.6401    0.2778    0.0821    0.0459

    0.0259    0.0376   -0.0116    0.0947

>> pinv(A)*A

ans =

    1.0000   -0.0000   -0.0000

   -0.0000    1.0000    0.0000

    0.0000    0.0000    1.0000

>> 

Resuelve_chol(A’A,A’b) es lo mismo que usar pinv(A)*b

Ejercicios:

1)

Dado el sistema:

2X1 + 3X2 – X3 = 7

-X1 +X2 +X3 =1.8

3X1 +X2 +X3=2.5

-X1 –X2 -2X3=2

2X1+X2+X3=1.2

I)                    Hallar Xcm la solución de cm con

a.       Cholesky

b.       Pinv

Y constatar que coinciden

II)                  Comparar AXcm con b

III)                 Hallar el error relativo de ||AXcm-b||/||b||

IV)                Generar 1 millon al azar de vectores (X1 X2 X3) y comprobar que ||AX-b||>=||AXcm-b||

V)                  Verificar que pinv(A)*A=I3 pero A*pinv no es I

2)

Tomar

A=randn(2000,1500);

B=randn(2000,1);

Hallar Xcm y calcular error relativo

i)                    Con Cholesky

ii)                   Con pinv

iii)                 Verificar si coinciden y hallar el tiempo de ejecución.

1)

I)

>> A=[1 3 -3; -1 1 1; 3 1 1;-1 -1 -2;2 1 1];

>> b=[7;1.8;2.5;2;1.2];

>> Xchol=resuelve_chol(A'*A,A'*b);

>> Xpinv=pinv(A)*b;

II)

>> A*Xchol

ans =

    7.3148

    0.2586

    1.3390

    0.1110

    1.0689

>> A*Xpinv

ans =

    7.3148

    0.2586

    1.3390

    0.1110

    1.0689

>> b

b =

    7.0000

    1.8000

    2.5000

    2.0000

    1.2000

III)

>> norm(A*Xchol-b)/norm(b)

ans =

    0.3404

>> norm(A*Xpinv-b)/norm(b)

ans =

    0.3404

IV)

>> cont=0;

>> for k=1:1000000

Xrand=randn(3,1);

if norm(A*Xrand-b)<norm(A*Xchol-b)

cont=1;

end

end

>> cont

cont =

     0

V)

>> pinv(A)*A

ans =

    1.0000    0.0000   -0.0000

    0.0000    1.0000    0.0000

   -0.0000    0.0000    1.0000

>> A*pinv(A)

ans =

    0.9850    0.0650    0.0305    0.0897    0.0391

    0.0650    0.6791   -0.2478   -0.3899   -0.0161

    0.0305   -0.2478    0.5917   -0.1829    0.3818

    0.0897   -0.3899   -0.1829    0.4618   -0.2346

    0.0391   -0.0161    0.3818   -0.2346    0.2823

2)

>> A=randn(2000,1500);

>> b=randn(2000,1);

>> tic

Xchol=resuelve_chol(A'*A,A'*b);

norm(A*Xchol-b)/norm(b)

toc

ans =

    0.5002

Elapsed time is 0.238292 seconds.

>> tic

Xpinv=pinv(A)*b;

norm(A*Xpinv-b)/norm(b)

toc

ans =

    0.5002

Elapsed time is 35.292501 seconds.

>> 

Tema de aplicación: Ajuste de parámetros con cuadrados mínimos.

Tendremos una serie de datos apareados (Xn,Yn) y buscaremos una función que explique los datos, para predecirlos.

Nosotros trabajaremos con funciones simples, conocidas, por ejemplo F(X)= 5 sen(X) + 2X

En general, serán funciones del tipo F(X)=L1F2 + L2F2 + … + LnFn con L coeficiente, F función simple conocida, y n un número lo menor posible para encontrar soluciones sensillas.

Generalmente ya conoceremos los Fs a los que intentaremos ajustar la función, por lo que el ejercicio será encontrar los L tal que la función compuesta de Fs se asemeje lo más posible a los datos.

Por ejemplo, F(X)=L1 sen(X) + L2 X

Buscaremos encontrar los valores L1 y L2 que más se asemejen a la serie de datos empíricos que son dados.

Matricialmente se puede expresar:

| F1(X1)    F2(X1)  …  Fn(X1) |   | L1 |         | Y1 |

| F1(X2)    F2(X2)  …  Fn(X2) |   | L2 |  =     | Y2 |

|  …            …..                   …..   .. ….   |        | ….  |

|  F1(Xm)  F2(Xm)  …  Fn(Xm) || Lm|         | Ym |

Si A es la matriz de Fs, L es la matriz de Ls, Y es la matriz de soluciones

A*L=Y

Ejemplo:

>> X=[0;1;2;4;7];

>> Y=[0.48;1.52;6.6;29;90.5];

>> plot(X,Y,'*')

>>

                          

Podríamos aproximar los puntos por distintas funciones, los datos parecen presentar un comportamiento cuadrático, pero cual función cuadrática se acerca mejor?

Usemos la técnica de cuadrádos mínimos para encontrar cual de todas las

F(X)=L1X^2 + L2X + L3

Mejor se ajusta a los datos de la tabla.

Entonces, estamos asumiendo que es cuadrática, es decir estamos fijando los parametros F de la matriz A, la función genérica planteada hace un rato, y estamos buscando los parámetros L tal que el ajúste por cuadrádos mínimos de un error relativo mínimo.

Planteamos entonces A=[X.^2 X X.^0]

(X.^2 X X.^0) (L)=(Y)

Y la solución:
L=pinv(A)*Y

L=resuelve_chol(A’*A,A’*Y)

En Matlab:

>> A=[X.^2 X X.^0];
>> L=pinv(A)*Y

L =

   1.9279
  -0.6038
   0.3201

>> L=resuelve_chol(A'*A,A'*Y)

L =

   1.9279
  -0.6038
   0.3201

>> f=@(X)L(1)*X.^2+L(2)*X+L(3);

>> plot(X,Y,'*',X,f(X),'O',0:0.1:7,f(0:0.1:7))

Proposición:

Busquemos ajustar los mismos datos por una lineal. Como queda? Cual es el error?

B1*X B2*1=Y

Buscar B1 y B2, y hallar el error relativo.

Luego hacer lo mismo con una polinómica grado 3.

1)

>> A=[X.^1 X.^0];

>> B=pinv(A)*Y;

>> f=@(X)B(1)*X+B(2);

>> norm(A*B-Y)/norm(Y)

ans =

    0.2241

>> plot(X,Y,'*',X,f(X),'O',0:0.1:7,f(0:0.1:7))

>> B

B =

   13.1669
  -11.2473

2)

>> A=[X.^3 X.^2 X.^1 X.^0];

>> C=pinv(A)*Y;

>> f=@(X)C(1)*X.^3 +C(2)*X.^2+C(3)*X+C(4);

>> norm(A*C-Y)/norm(Y)

ans =

 6.7189e-004

>> plot(X,Y,'*',X,f(X),'O',0:0.1:7,f(0:0.1:7))

>> C

C =

   -0.0227
    2.1615
   -1.1590
    0.4946